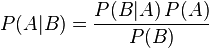Теорема Байеса
(или формула Байеса) — одна из основных теорем элементарной теории вероятностей, которая позволяет определить вероятность какого-либо события при условии, что произошло другое статистически взаимозависимое с ним событие. Другими словами, по формуле Байеса можно более точно пересчитать вероятность, взяв в расчет как ранее известную информацию, так и данные новых наблюдений. Формула Байеса может быть выведена из основных аксиом теории вероятностей, в частности из условной вероятности. Особенность теоремы Байеса заключается в том, что для ее практического применения требуется большое количество расчетов, вычислений, поэтому байесовские оценки стали активно использовать только после революции в компьютерных и сетевых технологиях.

читать дальше

Теорема Байеса названа в честь её автора Томаса Байеса (1702—1761) — английского математика и священника, который первым предложил использование теоремы для корректировки убеждений, основываясь на обновлённых данных. Его работа «An Essay towards solving a Problem in the Doctrine of Chances» впервые опубликована в 1763 году, через 2 года после смерти автора. До того, как посмертная работа Байеса была принята и прочитана в Королевском обществе, она была значительно отредактирована и обновлена Ричардом Прайсом. Однако эти идеи не предавались публичной огласке до тех пор, пока они не были вновь открыты и развиты Лапласом, который первый опубликовал современную формулировку теоремы в его книге 1812 года «Аналитическая теория вероятностей».
Сэр Гарольд Джеффрис писал, что теорема Байеса «является основой теории вероятности, точно так же как и теорема Пифагора есть основа геометрии» .

При возникновении теоремы Байеса вероятности, используемые в теореме, подвергались целому ряду вероятностных интерпретаций. В одной из таких интерпретаций говорилось, что вывод формулы напрямую связан с применением особого подхода к статистическому анализу. Если использовать байескую интерпретацию вероятности, то теорема показывает, как личный уровень доверия может кардинально изменить количество наступивших событий. В этом заключаются выводы Байеса, которые стали основополагающими для байесовской статистики. Однако теорема используется не только в байесовском анализе, но и активно применяется для большого ряда других расчетов.
Психологические эксперименты показали, что люди часто неверно оценивают апостериорную вероятность события, поскольку игнорируют его априорную вероятность. Поэтому правильный результат по формуле Байеса может сильно отличаться от интуитивно ожидаемого.

Формула Байеса:

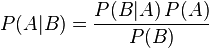
где
P(A) — априорная вероятность гипотезы A (смысл такой терминологии см. ниже);
P(A|B) — вероятность гипотезы A при наступлении события B (апостериорная вероятность);
P(B|A) — вероятность наступления события B при истинности гипотезы A;
P(B) — полная вероятность наступления события B.

Пример
Событие A — в баке нет бензина, событие B — машина не заводится. Заметим, что вероятность P(B|A) того, что машина не заведется, если в баке нет бензина, равняется единице. Тем самым, вероятность P(A) того, что в баке нет бензина, равна произведению вероятности P(B) того, что машина не заводится, на вероятность P(A|B) того, что причиной события B стало именно отсутствие бензина (событие A), а не, к примеру, разряженный аккумулятор.

Парадокс теоремы Байеса
При рентгеновском обследовании вероятность обнаружить заболевание туберкулезом у больного туберкулезом равна 0.9, вероятность принять здорового человека за больного равна 0.01. Доля больных туберкулезом по отношению ко всему населению равна 0.001. Найти вероятность того, что человек здоров, если он был признан больным при обследовании.
P («Б»|Б) = 0,9; Р («Б»|З)= 0,01; Р (Б) = 0,001, значит P (З) = 0,999; Р (З|«Б») — ?
Вычислим сначала полную вероятность признания больным: 0.999*0.01 + 0.001*0.9 =1,089 %
Вероятность «здоров» при диагнозе «болен»: Р (З|«Б») = 0.999*0.01 / (0.999*0.01 + 0.001*0.9)= 91,7 %
Таким образом, 91,7 % людей, у которых обследование показало результат «болен», на самом деле здоровые люди. Удивительный результат возникает по причине значительной разницы в долях больных туберкулёзом и здоровых. Туберкулез — редкое явление, поэтому и возникает такой парадокс Байеса. При возникновении такого результата лучше всего сделать повторное рентгеновское обследование.